A mathematician has just solved a 4,000-year-old Egyptian puzzle

"This may be the oldest math problem in human history."

As you may know, around 2000 BC, the ancient Egyptians were the first to use the concept of fractions. They denoted it with a hieroglyphic letter, like an eye without iris. Eg:

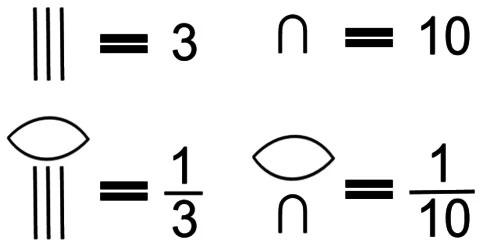
The concept of fractions was born that greatly helped the daily life of the Egyptians, such as distributing food or wages to those involved in the construction of the pyramids.

But there's a strange thing you don't know: Egyptian fractions rarely have numerators greater than 1, nearly all of the fractions they use are of the form 1/x. For example, if the ancient Egyptians had a bucket of water up to 3/5 full, they never divided the bucket into 5 parts and said it was 3 parts full.

Instead, the ancient Egyptians saw that the bucket was half full, plus 1 in 10. And it was true: ½+1/10 = 3/5.

The reason why the Egyptians used a fraction system with only 1 numerator is not clear. But miraculously, that system proved to be useless. Let's take an example: A janitor at the pyramid needs to divide 6 loaves of bread among 6 servants. But today, the payer said they only had the last 5 loaves of bread left. How to evenly divide those 5 breads?

If you use the fraction 5/6, you will have to cut each cake into 6 equal parts, after which each farmer will receive 5 portions. But the ancient Egyptians applied a simpler calculation with 5/6 = 1/2 + 1/3.

Thus, you will only need to cut 3 cakes in half, and cut the remaining 2 cakes, each into thirds. So each villager will receive half a cake and 1/3 more. Smart isn't it?

The ancient Egyptians realized they could always divide a pie into parts, which represented a set of fractions with a numerator of 1. For example, 1= 1/2 +1/3 +1/6. But it's also possible 1=1/2+1/3+1/7+1/42. 1= 1/2+1/3+1/12+1/18+1/36 as shown below:

This fact was summed up by mathematicians Paul Erdős and Ronald Graham as a problem in the 1970s: If given you a set of positive integers (that is, the latter is always greater than the former), just set large enough, you will always find a set of numbers where the sum of their reciprocals is 1:

Let's take an example of the set of consecutive even numbers see {2,4,6,8,10,12,…}. Oh no more counting, we've got 2,4,6 and 12: 1/2+1/4+1/6+1/12 = 1.

Now with the set of consecutive odd numbers {1,3,5,7,9,11,13,15,17…} it takes a bit of work, but miraculously, for you to press the calculator then:

The problem is simple, but proving it always true is not easy. "This could be the oldest problem in human history ever," said Carl Pomerance, a mathematician from Dartmouth College.

"I think the solution to this problem is impossible, no one will be able to find it. I myself don't see any clear approach to solving it," said Andrew Granville, a visiting mathematician. from the University of Montreal adds.

But surprisingly, recently a mathematician at the University of Oxford, UK named Thomas Bloom solved it in a very simple way. Bloom first read about the problem last September in a 20-year-old paper.

That paper belonged to a mathematician named Ernie Croot, who solved the so-called colored version of the Erdős-Graham problem. There, all the numbers were randomly arranged into different groups indicated by color: Some were in the blue group, others in the red group, etc. Erdős and Graham predicted that no matter what No matter how many different groups are used in this arrangement, at least one group must contain a subset of integers whose reciprocal sum is 1.

But Croot's solution required a series of complex mathematical methods such as harmonic analysis - a branch of mathematics closely related to calculus - to confirm Erdős-Graham's prediction. His paper was published in the Annals of Mathematics, a leading journal in the field - the very paper Bloom had read.

Also, when sorting numbers into groups, Croot wants to avoid composite numbers with large prime factors. The reciprocals of those numbers tend to add up to fractions with large denominators rather than reducing to simpler fractions that are easier to combine to form 1.

Thus, Croot proved that if a set has enough numbers with many relatively small prime factors, it must always contain a subset whose inverses add to 1. This suffices to prove the problem. Erdős-Graham coloring version.

But in its more general version, mathematicians cannot simply pick out the most convenient arrays of colors. They may have to find solutions for non-numerical arrays of small prime factors — in which case Croot's method doesn't work:

It wasn't until now two decades later, when Bloom looked back at Croot's problem and solution, that he realized he could develop the technique Croot introduced in a simpler but more general version.

"I thought, wait, Croot's method is actually more powerful than I originally imagined. So I studied it for a few weeks, and as a result, this better solution was born," Bloom said. .

Croot's proof is based on a form of integral called exponential sum. It's an expression that can detect how many integer solutions to a problem — in this case, how many subsets contain the sum of unit fractions equal to 1.

Bloom has adapted Croot's strategy to work with large primes, simply by dividing 1 into fractions as small as 3 times 1/3. Now, instead of the problem of finding the sum of fractions with numerator 1 and sum 1, it becomes finding 3 sums of fractions whose numerator is 1 and sum is 1/3.

Then Bloom simply repeated Croot's method without now ignoring large primes. Bloom's method gave him finer control over those parts of the exponential sum, and as long as a set contains a small fraction but the sequence is large enough—no matter how small the fraction—it always doesn't. avoid finding sums equal to the unit fraction itself.

"This is an excellent solution," said Izabella Łaba, a mathematician from the University of British Columbia. "Combinative number theory and analysis have evolved a lot over the past 20 years. We return to the old problem with a new perspective and with more effective solutions.

With his new solution, Bloom has now completely proven a problem that dates back to ancient Egypt. But this is not the end of a story spanning more than 4,000 years.

Bloom says the problem can continue to evolve because modern number theory is still evolving. "I'm currently working on formalizing evidence in Lean, what's known as 'evidence assistant'," he said. "This is an exciting new field where we have computers to formally test proofs at a much more rigorous level than basic human mathematics."

A new problem arises in it: Can you find some infinite set of positive numbers, without being able to find any group of inverses whose components sum to 1?