How to measure how long Fidget Spinner rotates without a clock

Why? Because obviously the watch is not available but the laser device and light sensor are sold in the market .

The toy to fidget Spinner's hand is a new trend of young people, descended from Rubik's blocks, of the electronic game set 9999in1, Tamagotchi's virtual chickens . You see it appear. everywhere, from the surface of the street to every newspaper, you wonder where to buy one to come back because they look good .

That fame prompted the assistant professor of physics Rhett Allain at Southeastern University of Louisiana to study how long this Fidget Spinner (FS) could rotate. First, Allain points out that the time that the FS can rotate will be based on its angular velocity. First, understand the basic rotation. For example, we have an object centered around a bicycle wheel (below), we can determine the corner position at any point, and call that angle θ.

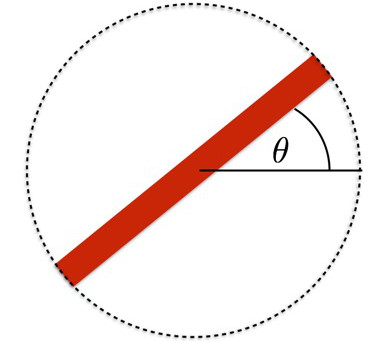
If this wheel continues to rotate so that the angle θ changes, we can describe the rate of change of angular velocity with the symbol ω. This is the recipe for finding the average angular velocity of the wheel:

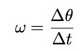
It looks very much like the usual constant velocity calculation. But what if the object turned around or slowed down? So the change in angular velocity will be denoted by α, calculated by the following formula:

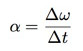
If we know the initial angular speed of the rotating object and we assume the final rotation velocity of the object is 0 radians per second, we will get the object's rotation time formula:

Now we need an angle acceleration - assuming it's always fixed when the device rotates slowly. We can calculate angular acceleration based on the change of angular velocity, even though it is not easy to measure at all. The FS device rotates so fast that it can spin (or at least the high-speed camera of Allain's assistant is not "good" ), so we will use a laser system to measure the change of velocity corner.

The upper part is the laser transmitter, and the lower part is the light sensor.

The basic mode of operation of this system is the laser light illuminating the light sensor below. When the FS rotates, it blocks the laser light every time the FS's wing rotates through the light. The value that the light sensor will measure is the rotating ratio of the FS device.

But this system also has some minor problems. First, the speed of the flashing light changing on the light sensor will be different from the rotation speed of FS, because on this rotating device there are 3 small holes, creating gaps in each rotation that the laser can through. Second, FS will rotate very fast and lots of loops, the amount of data collected will greatly slow down the analysis process.

This is a piece of data obtained:

This will be a more interesting trick than numbers and dry calculations. Instead of sitting analyzing a large data sheet of time and light (the total data is up to more than 2 minutes, but above is only 0.15 seconds), Allain's assistant professor will apply the maritime license. Fourier.

Explanation : Fourier transform allows us to convert a function or a time-domain signal to a frequency domain. Since this number of data is made up of many different trigonometric factors (such as sin and cos) with different measurements, their amplitudes will be different. Fourier transforms will show different amplitudes, so that we can find the oscillation frequency.

Taking a small part of the laser data, we will have the following Fourier transform operation:

With the vertical axis is the Amplitude and horizontal axis is the frequency (in Hz).

The maximum point at 20.14 Hz is the rotation amplitude of the FS device (at the time of the first measurement). Other bouncing points next to it need not be concerned at the moment. To determine the angular velocity, we only need to multiply this frequency by 2π and we get a speed of 126.54 radians per second.

What if we create a Fourier transform for all the light data that lasts more than 2 minutes? We will have a great milestone and that data will not help much. Instead, Associate Professor Allain will break up parts of the data and find out the corner speed. By subdivision, the angular speed is almost a constant. As a result, we can create a graph that shows angular speed:

The slope in the graph is the angular acceleration with the value of -1,346 radian / s ^ 2, and because this data has a stable route, we can have angular acceleration at all times almost a constant. Then, we can find out how long this device can rotate.

With an initial angular velocity of 140 radians per second (slightly faster than the above data), FS will rotate within 104 seconds. If you want to rotate it longer, just rotate it . faster. Duplicating the initial speed, you'll double the Fidget Spinner's rotation time.

You have a little more useful information! Fidget Spinner is just as useful as the device itself.