Mathematician solves 150-year-old super-difficult chess problem
Chess is an ancient game originating from India and Persia, which began to appear in Southern Europe from the second half of the 15th century. Despite its long existence, chess still has many mysteries, in The most famous is the n-queen (n-queen) problem, which comes from a puzzle.

Chess is an ancient game that originated in India and Persia.
The puzzle is as follows: Ask how many ways in which 8 queens - the strongest pieces on the board and capable of moving any number of squares horizontally, vertically and diagonally - can be positioned on a standard 64 square chess board with no queens in a position to "get in the way" of each other.
The above puzzle first appeared in 1848, posed by grandmaster Max Bezzel in the chess magazine Schachzeitung, Germany. From the moment it was mentioned, the puzzle has made it difficult for many chess enthusiasts to solve it, and even mathematicians.
The answer was revealed 2 years later, with the answer being that there are 92 ways to arrange 8 queens on the chessboard, but if summed up, there are only about 12 basic layouts, because the words Most of the remaining solutions are symmetrical.
But in 1869, a variant of the above puzzle was presented by the mathematician Franz Nauck, and it was even more puzzling. Problem asks: Instead of placing 8 queens on a standard 8 x 8 board, what if for 1,000 queens on a 1,000 x 1,000 board? Next is 1 million, 1 billion.
What was once a relatively simple puzzle has become a much deeper problem, when it requires discovering a general rule for the number of possible arrangements of positions of any number (represented as "n". ") of the queens on the coefficient nxn .
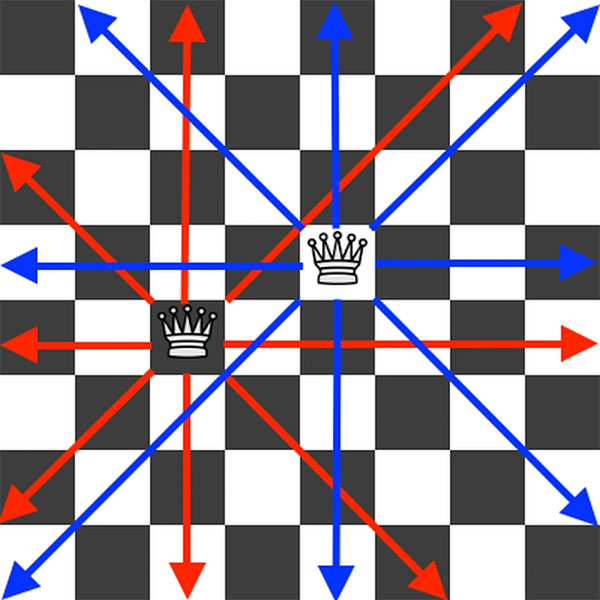
The problem involves placing queens on the chessboard so that piece A is not in the path of B's move/attack.
It is not until now, after more than 150 years, that Michael Simkin, a mathematician at Harvard University's Center for Applied and Mathematical Sciences, has given the answer that is considered to be almost correct. .
Specifically, according to Simkin, on a giant chess board with coefficient nx, with about (0.143n) ^ n ways to arrange n queens such that no air can attack each other. That means on a million x million chessboard, the arrangement of 1 million queens can amount to a number of 5 million zeros.
It is known that it took Simkin nearly 5 years to find this approximate equation. His way of solving the problem was to place a random queen on the board, then block every tile it could reach (including vertical, horizontal and diagonal tiles). Then, they continue to use the algorithm to arrange the remaining queens in the same way.
However, this algorithm is far from perfect, as it only works best on symmetric problems, where every square provides an attacking advantage to the queen just like any other square. Meanwhile, this is not the case for a standard chessboard, where queens on the square close to the border are much less likely to attack than the squares in the center.
To solve the problem, Simkin realized he would need to make further tweaks to the algorithm, but was closer to conquering this challenge.
"I think personally I might be able to solve the n-queen problem in a while," Simkin said. "Not because there's nothing left to do, but just because I've always dreamed of variations of chess and I'm ready to continue my passion."
- A mathematician just solved the 160-year-old problem worth $ 1 million
- The international press has a headache with Vietnam's super-difficult grade 3 problem
- Trying with the problem of 263 years, there is no right answer
- Robot chess board
- New-style chess: two players fight at the same time, each piece has its own
- The chess player costs £ 1 million in a 55-year drawer
- 16-year-old student conquered the century problem
- Chess board is extremely unprecedented unprecedented: designing a sphere and using magnets to control chess pieces
- The super-difficult problem that existed for decades has been solved, the solution weighs 200TB
- The prize was awarded to the postman on the board, winning 1 million dollars in bonuses
- The ability to play chess is
- Are you among the 20%
 The most famous scientific failures in history
The most famous scientific failures in history Mysterious genius mechanic and the machine froze time
Mysterious genius mechanic and the machine froze time The son carries the 'bad gene' of genius Albert Einstein
The son carries the 'bad gene' of genius Albert Einstein Isaac Newton
Isaac Newton